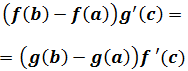Teorema del valor medio de Cauchy

En análisis matemático, y más concretamente en cálculo diferencial, el teorema del valor medio de Cauchy es una generalización del teorema del valor medio (de Lagrange). A partir de este puede demostrarse la regla de L'Hôpital, fuerte ayuda para el cálculo de límites con indeterminaciones ${\displaystyle \textstyle {\frac {0}{0}}}$ o ${\displaystyle \textstyle {\frac {\infty }{\infty }}}$.

Enunciado

El teorema, aparecido en su Cours d’Analyse (1821),^[1]​ se enuncia de la siguiente manera:

Nótese el caso particular en el cual g(x)=x, donde entonces la expresión se reduce al teorema del valor medio de Lagrange.

Demostración

• Sea G(x) una función definida como:

${\displaystyle G(x)=[g(b)-g(a)]\cdot [f(x)-f(a)]-[f(b)-f(a)]\cdot [g(x)-g(a)]\,\!}$

donde f(x) y g(x) son funciones continuas en [a,b], derivables en (a,b). Se puede observar por simple inspección que G(a)=0 y G(b)=0.

• Por el Teorema de Rolle, existe un c, perteneciente al intervalo (a,b), tal que G'(c)=0. Así, derivando G(x) se obtiene:

${\displaystyle G'(x)=[g(b)-g(a)]\cdot f'(x)-[f(b)-f(a)]\cdot g'(x)}$

y sabiendo que G'(c) es 0

${\displaystyle 0=[g(b)-g(a)]\cdot f'(c)-[f(b)-f(a)]\cdot g'(c)}$

de donde se deduce que

${\displaystyle [f(b)-f(a)]\cdot g'(c)=[g(b)-g(a)]\cdot f'(c)}$

• Si g(b)-g(a) y g'(c) son distintos de 0, la expresión anterior puede ser escrita como:

${\displaystyle {\frac {f(b)-f(a)}{g(b)-g(a)}}={\frac {f'(c)}{g'(c)}}}$

Q.E.D.

Consecuencias

El teorema de Cauchy es usado para la demostración de otros teoremas. Nos permite, entre otros, demostrar la regla de L'Hôpital:

${\displaystyle \lim _{x\to c}{\frac {f(x)}{g(x)}}=\lim _{x\to c}{\frac {f'(x)}{g'(x)}}}$

muy usada en análisis matemático, para el cálculo de límites de la forma de ${\displaystyle \textstyle {\frac {0}{0}}}$ o ${\displaystyle \textstyle {\frac {\infty }{\infty }}}$.

Referencias

• Trott, Michael. «Mean Value Theorem». The Wolfram Demonstrations Project (en inglés). Wolfram Research. 
• Weisstein, Eric W. «Teorema del valor medio». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
• Weisstein, Eric W. «Teorema del valor medio de Cauchy». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.